3장의 목적:
(기저대역 신호의 복조와 검출)
수신기가 받은 신호의 파형은 이미 pulse 형태를 가지고 있다. 하지만 복조(demodulation)과 감지(detection) 과정을 거치는데,
그 이유응 송신기와 채널의 필터링 과정에서 기저대역의 펄스가 상호간섭을 받게 되면서 "smearing(퍼진)" 형태의 신호가 되어서 샘플링과 검출 과정에 적합하지 않다(=원신호와 오차가 큰 신호로 복원이 될 수 있다).
따라서 복조기는 신호 대 잡음비(SNR, Signal to Noise Ratio)가 최대한 좋은 상태의 기저대역 펄스를 복원하는 것을 목표로한다.
-> 균등화(Equalization): 이 채널에서 발생하는 간섭을 보정하는데 사용된다.
---
1. channel impairments
- 열잡음
- 전자의 열 운동 때문에 amplifier, 회로에서 신호가 오염됨
- 가우시안 확률 분포 + zero-mean 의 정규분포
- 백색 잡음(White Noise), 전 주파쉐서 동일한 파워 스펙트럼 밀도를 가짐 == 저주파수와 고주파수에서 동일한 전력 밀도를 가짐

2. Binary Baseband system에서 신호모델

- 수신 신호 모델(노이즈 AWGN 및 ISI 채널 왜곡 포함)

- 수신 신호 모델(AWGN만을 포함)
이상적인 채널이기 때문에 h(t)가 임펄스 형태이므로 컨볼루션 영향이 없어진다.
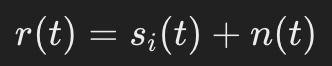
- 송신기 및 수신기의 필터링 과정에서 신호가 왜곡됨 -> ISI(Inter-Symbol Interference)
3. Demodulation과 Detection과의 차이?
- 복조는 왜곡되지 않은 기저대역 펄스로 신호를 복원하는 것
이진 형태(bit)의 binary 신호를 waveform 의 symbol로 mapping하는 과정을 복조라고 하며 반대(demapping)하는 과정은 de-modulation 이라 한다.
- 검출은 디지털값(0 or 1)을 결정하는 과정으로, threshold 비교를 수행하여 1 이나 0을 결정한다.
---
4. 디지털 신호의 복조+검출 2step

- Receiving Filter: 필터 출력의 SNR 을 최적화한다.
- Equalizing Filter: 채널에 의해 발생한 ISI 최소화한다.
1) Step1: Waveform-to-Sample Transformation(복조 및 샘플링)
- z(T)는 복조기와 샘플러를 거치며 필터링 후 샘플링된 결과값이다. Baseband pulse 로 볼 수 있다.
- 입력신호 s(T)를 필터링한 후, 각 심폴 간격 t=T에서 샘플링하여 predetection point 에서 통계랑 z(T)를 가진다.
-> ai(t)는 원하는 신호 성분이 필터를 거친 결과, n0(t)는 AWGN이 필터를 거친 결과
-> ai(t)는 특정 샘플링 시점 T에서의 값이기 때문에 프로세스가 아닌 랜덤변수이다.
- 이 값은 전압 Volatage(2nd-order value)로 해석되는데, 이는 수신 심볼 에너지와는 비례하며 잡음의 영향과는 반비례하다.

- ai(T)와 n0(T) 둘 다 가우시안 랜덤 변수로 두 개의 합인 z(T) 또한 가우시안 랜덤변수이다.
- 디지털 신호는 0 또는 1의 두가지 상태만 가지기 때문에 a는 a1 또는 a2만 가짐
2) Step2: Decision Making(결정과정)
- 검출기에서 샘플링된 값 z(T)을 바탕으로 신호를 해석해서 디지털 신호로 결정한다.
- 임계값을 기준으로 z(T)가 큰 경우 s1, 작을 경우 s2 를 선택하는 방식.
---
신호와 노이즈의 벡터적 관점
---
2. white noise 의 표현
화이트 노이즈 n(t) 는 신호공간 안의 성분과 신호공간 밖의 성분으로 분해할 수 있다.

n^(t)은 신호 공간 내의 기저함수 ψj(t) 로 표현되는데, 이 때 nj는 노이즈의 신호 공간 안에서의 성분 계수로 주어진다.

즉, 신호 공간 내의 노이즈 각 차원별 성분 nj는 기저함수 ψj(t)에 대한 내적, 직교 투영(projection)으로 구하는 것이다.
nj는 서로 독립적인 확률변수이며 가우시안 분포를 가진다.
신호 공간 외부의 노이즈는, 전체 노이즈 성분에서 신호 공간 내의 노이즈 성분을 뺀 값이다.
이 값은 신호공간의 기저함수와 직교 관계(orthogonal)를 가진다. -> 신호공간 밖의 노이즈 성분은 신호 벡터에 영향을 주지 않는다.
3. white noise 의 분산
이론적으로 화이트 노이즈 n(T)는 모든 주파수 성분을 가지는 신호이므로 분산이 무한대이다.

하지만 유한한 대역폭의 필터를 거친 화이트 노이즈는 분산이 N0/2 로 제한된다!
-> 노이즈의 특성을 파악할 때 유한한 값을 고려해야하므로 중요한 특징으로 고려함


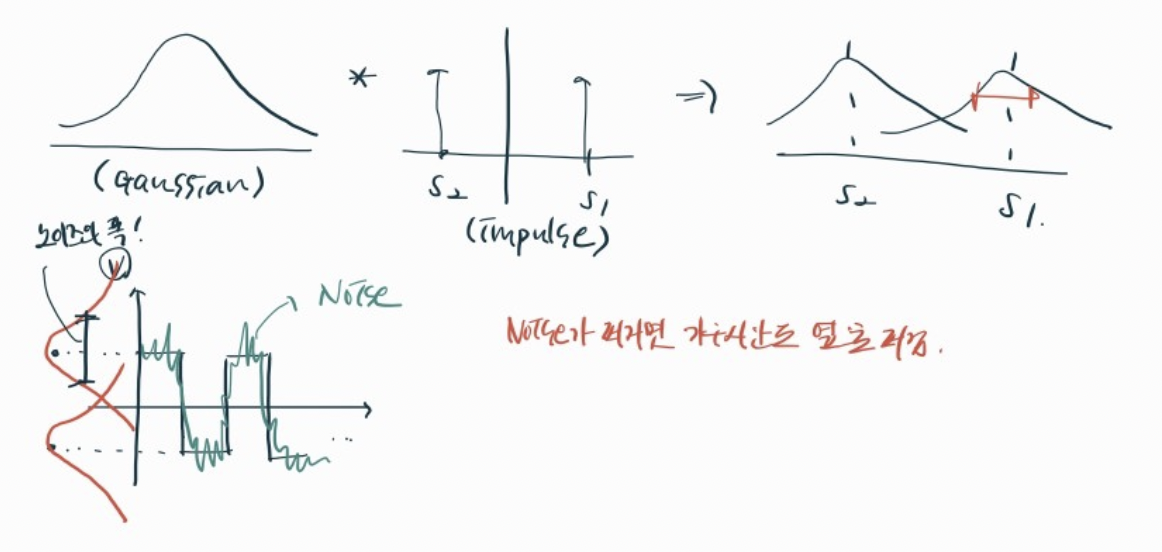
위의 필기는 신호 symbol 검출(Detection) 과정에서 수신 신호가 노이즈 영향을 받아서 확률분호 형태로 변하는 과정을 정리한 것이다.
왼쪽 가우시안은 노이즈 n(t)를, s1과 s2의 impulse 신호는 전송된 신호를 의미한다.
가우시안 노이즈와 신호(Impulse)를 컨볼루션하면 각 신호 s1, s2가 가우시안 확률분포를 따르는 형태로 변환되는것이다!
때문에 s1과 s2는 명확히 구분되지 않고 겹치는 부분이 생기는데, 이 영역이 바로 오류 발생 확률 영역을 의미한다.
---
4. 디지털 통신 시스템에서 SNR 파라미터
SNR(신호 대 잡음비) 는 평균 신호 전력 대비 평균 잡음 전력의 비율을 의미한다.
일반적으로 Eb/N0 을 사용하는데, 이는 정규화된 SNR로 비트 에너지/전력 스펙트럼 밀도를 의미한다.
Eb(비트에너지): 신호 전력 S와 비트 지속시간 Tb의 곱 -> 데이터 전송속도 Rb=1/Tb
N0(잡음 전력 스펙트럼 밀도): 잡음 전력 N/대역폭 W
S/Rb -> 단위 비트당 power
N/W -> 단위 주파수당 power
따라서 Eb/N0 는 단순히 S/N을 대역폭과 비트속도를 이용해서 정규화한 공식으로, 단위 주파수당 비트 power를 의미한다.



디지털 통신에서 바이너리 신호 검출
1) Maximum liklihood(ML) 수신기 구조
- Liklihood ratio test
: 두 신호 s1(t)와 s2(t) 에 대해 수신된 신호의 확률밀도함수가 각 s1과 s2가 송신될 사전 확률 P(s1), P(s2)와 비교됨


2) 최적 임계값
- 이상적인 경우 최적 임계값 r0은 두 신호의 평균값임


각 입력신호 s1과 s2가 송신될 사전 확률의 값이 1/2로 동일하고(= 수신기는 어떤 신호에 편향될 일이 없음)
조건부 확률밀도 함수 pdf가 대칭적일 때 임계값이 최적이다.
따라서 최적 임계값이 r0으로 결정되었을 때, 필터링 및 샘플링됨 값 z(t)가 r0보다 ㅋ면 h1 -> s1이 수신됨, 작으면 h2 -> s2가 수신되었다고 판단한다.


노이즈가 섞인 수신 신호를 구할 때, 수신신호 z가 있을 때 송신신호 s1가 전송될 확률인 P(s1|z)은 P(z)를 모르기 때문에 측정할 수 없음
-> MAP 문제 -> (sol) -> ML 검출기 -> P(s1|z)를 직접 구할 수 없기 때문에 Liklihood 함수인 P(z|s1) 을 이용해서 채널 모델(AWGN) 등을 유도할 수 있기 때문에 쉽게 계산 가능하다. 구한 뒤 베이즈 정리를 통해 P(s1|z) 를 구한다.
---
Error Probability, 오류 확률
- s1 이 전송되었으나 오류가 날 확률:

- s2가 전송되었으나 오류가 날 확률:

즉 전체 비트의 오류 확률인 Pb:

가우시안 정규 분포에서 임계값 r0(a1+a2/2)이상의 확률을 구한다면? -> 꼬리 확률을 구해야함 -> Q함수 이용
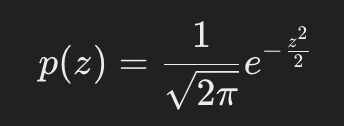
표준 정규 분포(평균이 0, 분산이 1인 가우시안 분포)의 확률밀도함수 PDF 는 위와 같은데, 이는 지수함수이므로 가우시안 분포의 꼬리(Tail) 영역의 확률을 표현할 수 있다. 이상적인 경우로 s1 과 s2의 사전 발생 확률이 같다면(=Optimal detection일 경우) 아래와 같이 유도된다.

'신호처리' 카테고리의 다른 글
| SNR, Matched Filter (0) | 2025.04.08 |
|---|---|
| [디지털 통신] Auto-correlation (0) | 2025.03.13 |
| [신호및시스템] review (0) | 2025.03.06 |
